Optimistic Parallel Order Books

As someone who’s background lies almost exclusively in creating parallel programs, I find a rule of thumb used at my current company (LMAX Group) to be deeply upsetting: When it comes to threads, if there’s more than one, there’s probably too many. In an act of bold defiance, I am going to enact my revenge on this outrageous rule by making parallel the very thing they hold dear.

We will be turning our perfectly servicable sequential order books, into multi-threaded monsters.

Determinism and Order Books

The key to any good order book is fairness. If I place an order on the book before you do, provided there are no delays being applied to my account, I should get to match against the passive orders on the book before you do. No matter how many times this scenario plays out, the outcome should be the same. If I arrive first, I should match first, this is the essence of determinism, and its vital to running an exchange fairly.

Here lies our first problem with making an order book run in parallel. With multiple orders arriving on the book at the same time through different threads, how can we ensure that my earlier order matched before yours does?

First things first, we need to know who actually arrived in the exchange first. This is quite simple. All orders have a timestamp of when they arrived. But this in and of itself does not solve our fundamental question of how this can be parallelized. We still need to run the orders through the matching engine in timestamp order right? Which would require us to run through the book sequentially right? Well actually, no, not really. It just requires us to re-frame how we think about what order books are.

Order Books as Discrete Event Simulations

If we look at the interaction of orders on an order books happening at deterministic times, we find that there is a striking similarity to another kind of program, a discrete event simulator. Fundamentally, the difference between how an order book works and how a discrete event simulation works are overwhelmingly small.

• In order books, we have orders which are executed in timestamp order one at a time, changing the state of the book.
• In discrete event simulations, we have events which are executed in timestamp order one at a time changing the state of the simulation.

If anything an order book is simpler, because orders are not capable of spawning off new orders the way events in discrete event simulations (DES) can.

None of this is sounding much like parallelism yet!

I’m getting there I promise!

Luckily, now we’ve framed our order book as a discrete event simulation, we can now take advantage of the huge wealth of research that has been made in DES, including what we will look at today: Optimistic Parallel Discrete Event Simulations (specifically Time Warp Simulation).

Have you got something to run on that billion dollar computer?

Unsatisfied with just making multi-thousand core super-computers, some people thought it might be a good idea to create massively parallel simulations for them to run. In a parallel simulation, each node in the system represents some small part of the simulation, and overall you can speed up the system through parallel execution…except, don’t these nodes need to communicate?

Let’s take the classic airport example that is so often looked at in this field of study. If I am simulating a network of airports, I may need to send a plane from my JFK node to the LAX node to say:

Please handle this plane which is going to arrive at LAX at 3pm, traveling from JFK

This kind of message actually creates a massive headache for using parallelism to speed up deterministic simulations. Because there is no way of knowing in advance that JFK is going to send a plane to LAX, it means that we cannot let our simulation of LAX advance its clock beyond the time of JFK without risking an event arriving in the past, and causing the simulation to crash. The only way that we could safely run our simlulation, is by only ever letting our nodes run in parallel if they hold events that happen at the exact same time. Naturally however, given the low probablity that planes take off at the exact same time, (or orders occuring at the exact same time…this likely not even being desirable) this is going to give us rather pathetic speed up over a sequential system. Nothing close to what we’re really looking for.

In reality, for this kind of simulation (called conservative parallel discrete event simulation <- my goodness aren’t academics imaginative) there are actually ways to solve this dilemma without resorting to the horrors of speculative execution which will follow. But we’re down the rabbit hole now, we may as well dig a little deeper.

If at first you don’t succeed, Try, try again

So what is the optimistic way of dealing with an event that happened in the past? Well…pretend it didn’t. Let the LAX node simulate beyond JFK and then when the event comes in, roll the clock back to 3pm and discard any state changes produced by events that happened after this point. Now that is easier said than done, and the systems used to allow a simulation rollback are significantly more in depth than I have time to go into in this article (Don’t worry, there’s a book recommendation at the end for the inquisitive mind), but please trust me when I say, it can be done.

So how can we apply the technique of optimistic parallelism to our order book example?

Let us try a naive approach initially:

• As orders come in, we will distribute them across our simulation nodes.
• Nodes will then have their own copy of the order book which they will run their orders through.
• If it turns out another node modified the order book in the past, the node will rollback its own order book to that point, applying the missing state, and try again.

Unfortunately this would fundamentally be no better than a sequential system:

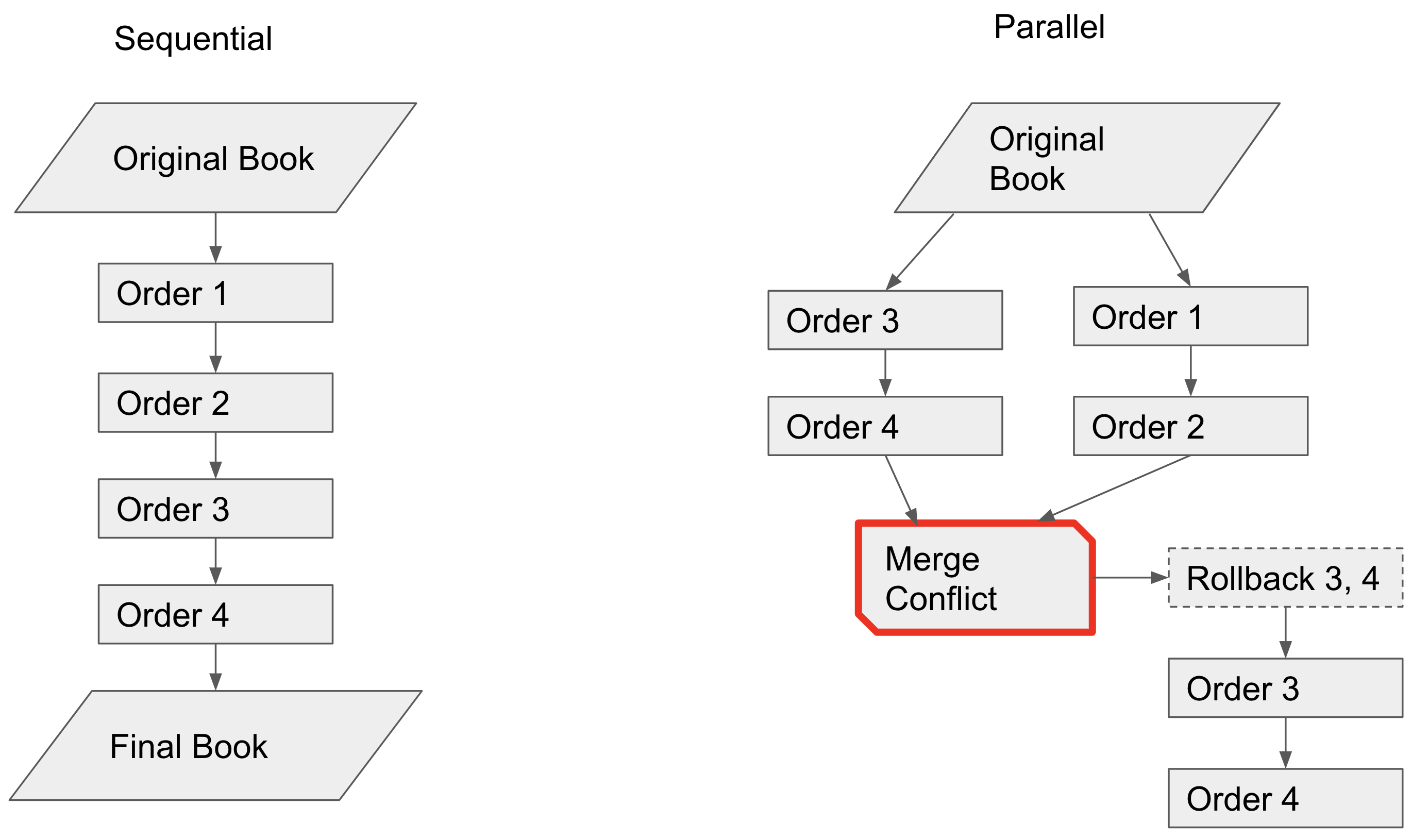
There would always be a clash when attempting to run the nodes in parallel, and orders would constantly get rolled back until everything becomes effectively sequential.

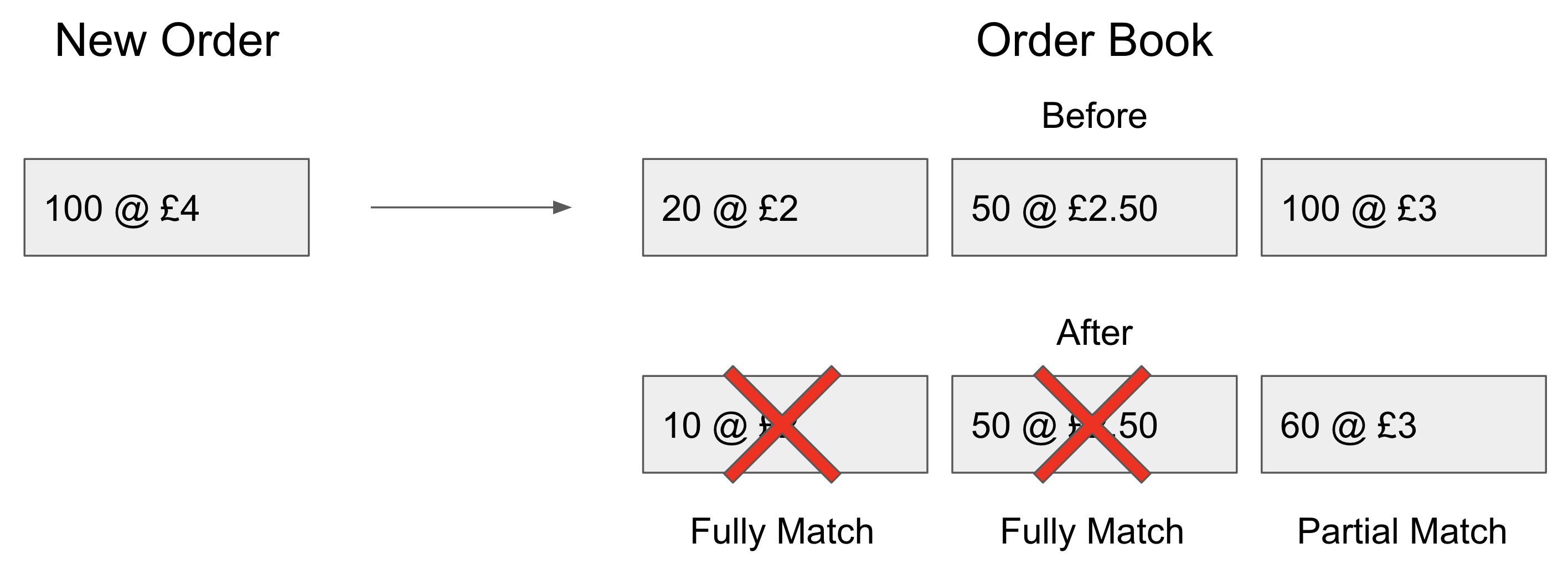
So instead, we have to do something a little more crafty, with a bit of domain knowledge about how orders are actually matched on the book. Fundamentally, an order book is just a set of two lists. One with orders from sellers, the other with orders from buyers. When a new order comes in, we will attempt to match it against existing orders on the book of its opposite side. But an order does not always match fully against one other order. If I have an order to buy 100 apples off of the book, the top order on the book may only have 20 to sell. This is not a problem, we will just match against the next order, and so on, and so on, until all 100 apples have been bought:

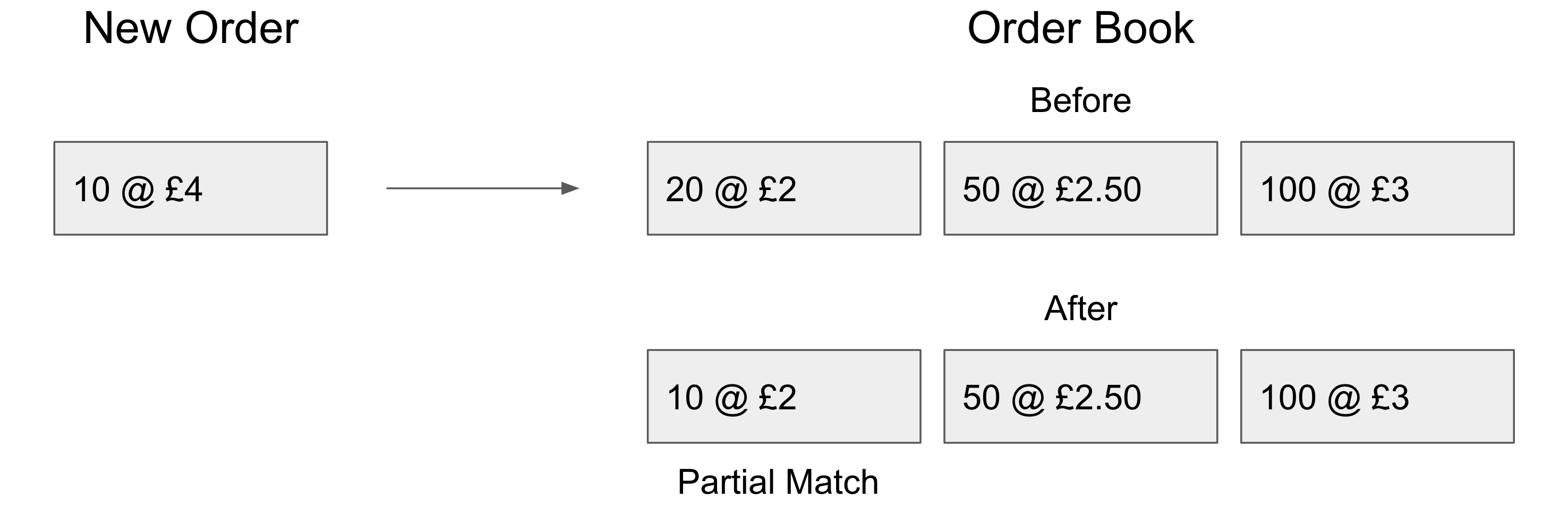
So how can we use this to our advantage for parallelism? Well the key is in there being multiple matches. Just because an order came in first, does not mean that it will fully affect the result of the match from the second order. Let us consider an example. I’m feeling cheap so I place an order for only 10 apples:

Now if you come in second with an order to buy 100 apples, the resulting execution is not actually that much different to if your trade had come before mine:

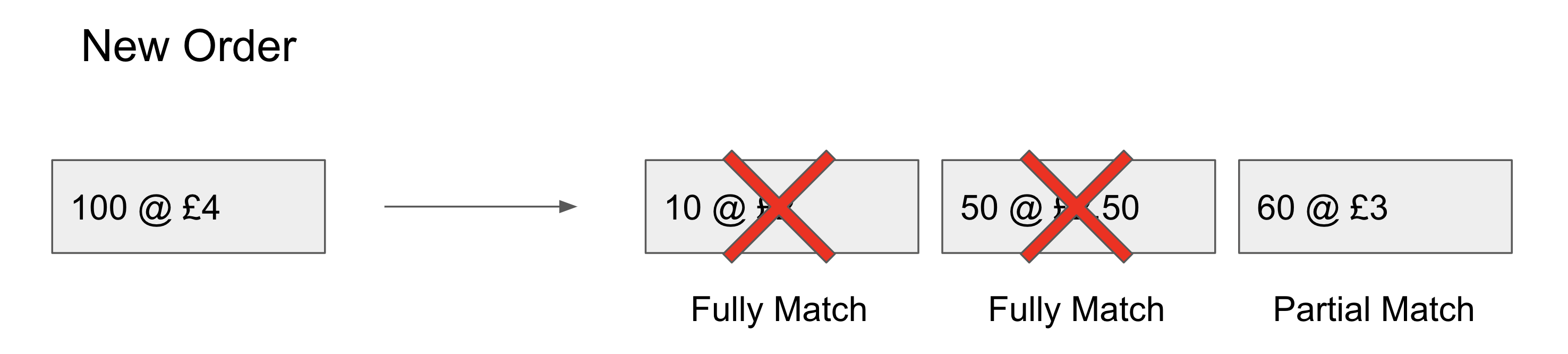
My trade didn’t even have any effect on your second match. It turns out its quite easy to take advantage of this minimal execution change by employing what I would term to be rollbackable data structures. Rollbackable data structures take account of the simulation time stamps of when it was accessed by different nodes, and facilitates rollbacks for nodes that access the same part of the structure out of time order.

In the case of the sell side of our order book, we’ll start with a fresh copy of our liquidity, and initialize the access time on each element to 0:

I place an order at time 50, your order arrives at time 100. Let us consider the correct execution order first, my order enters the order book first:

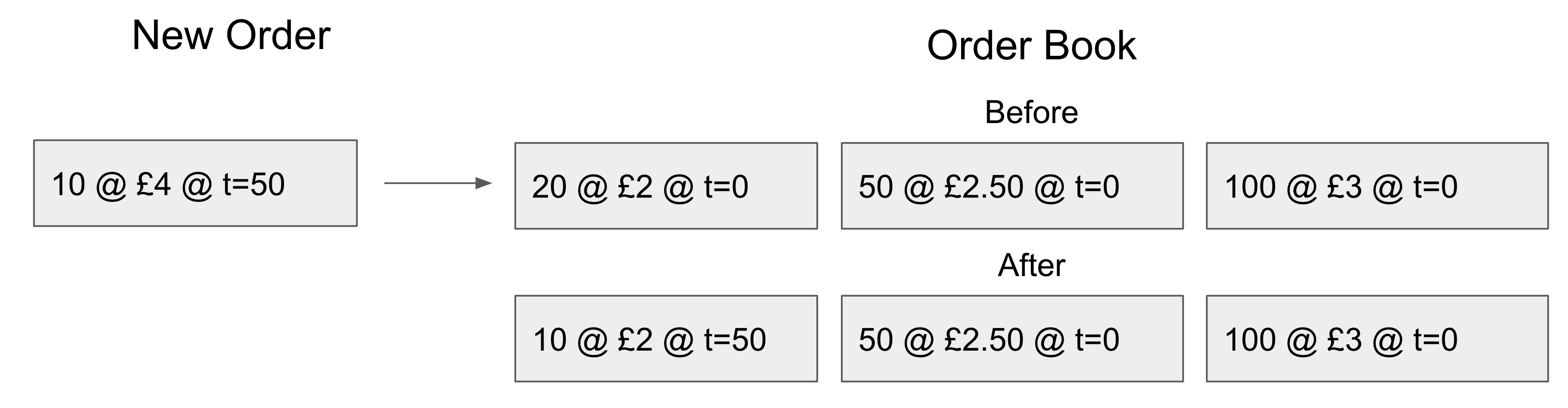
Notice that only the time of the £2 element gets updated to the time on my order. This is important for executing in the wrong order which we’ll look at later. Next your order is executed:

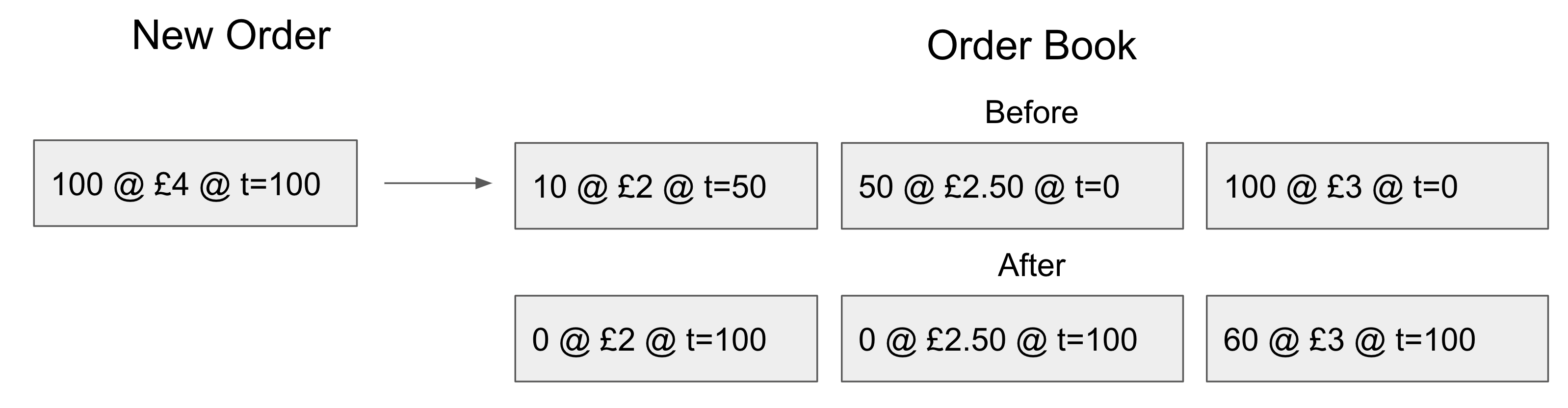
Because this executed in the correct order, no rolling back was required. The program could deduce this by looking at the timestamps on the list elements, which showed that our order was later than any of the orders that have been matched previously on that part of the book. Now lets try the same thing again but with the incorrect time order:

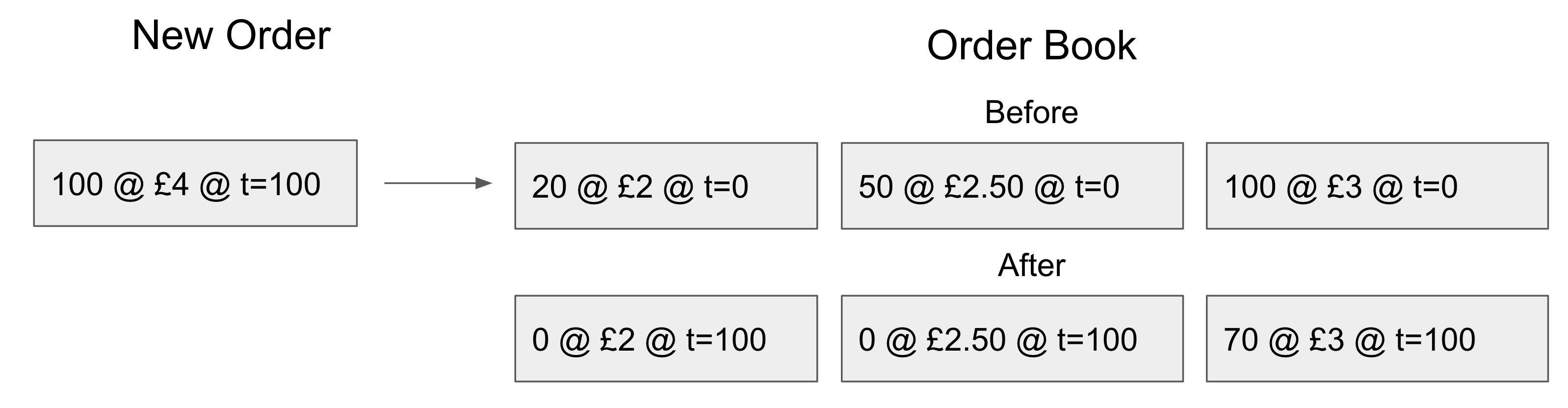
At this point, part of our execution is wrong and will need to be rolled back as the earlier trade gets matched:

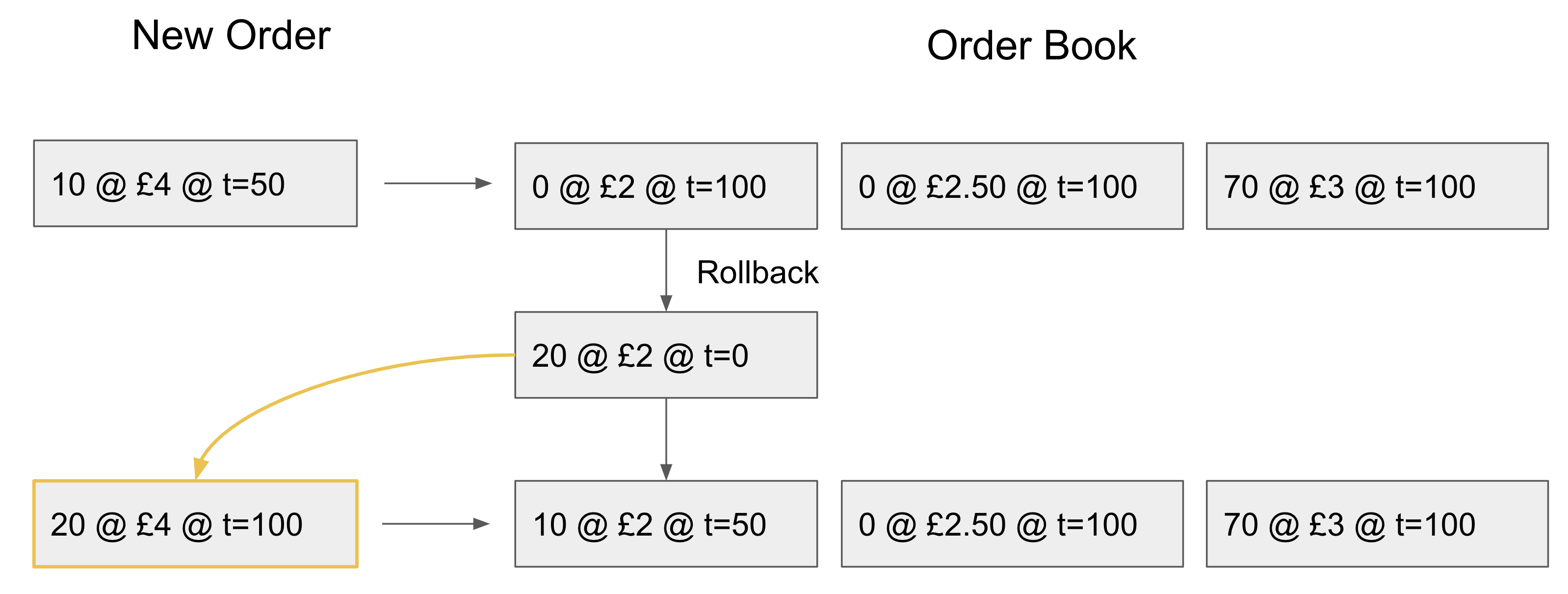
Now we will need to rematch the last 20 of the late order which got rolled back:

Naturally a further optimization could be made by only rolling back the part of the order which cannot be filled by the left over liquidity of the currently targeted element.

Can this actually give any performance benefits over sequential execution?

Its fair to say that attempting to evaluate the performance of a system without having even built it is often an exercise in futility, but we can attempt to reason about some of the benefits or drawbacks of this approach. The major performance gain that can be made with this approach is that matching for multiple aggressive orders can be made in parallel.

Consider a system that has relatively slow matching logic, and an order comes in which eats up a considerable amount of the liquidity on the book:

As is seen in this sequential example, the first order is taking a significant amount of time going through the book, and is blocking the execution of subsequent orders, which have no dependence on the first order’s later matches When running on a parallel order book, both can be executed at once giving some speed up:

This is of course best case scenario, where our executions happen in order, with no requirements for roll backs. If roll backs are expensive and out of order execution does occur, then it is entirely possible for the parallel order book to take even longer than the sequential book.

Another significant disadvantage of running an order book as an optimistic time warp simulation (the name given to simulations that have this roll back capability) is the same as every other time warp simulation. Eventually you will need to stop speculative execution and actually commit to a deterministic set of unrollbackable events, so that IO operations can be performed, and memory being used to store roll back states can be freed. This is done by calculating the global virtual time, which is the minimum time that any part of the simulation could be rolled back to. It turns out that this tends to be quite an expensive operation, and in a system where low latency is important, this could be a key factor in whether this can be effective of not.

Typically parallel discrete event simulations require considerable periods of time where nodes are not required to communicate, so its effectiveness on an ordinary order book is likely to be diminished. In books where the matching logic is quite restrictive, and additional optimizations can be placed on when the data structure issues roll back operations, it should be possible to provide speed up when orders with matching similarities are placed on the same node, reducing the frequency of cross node order matching.

Evaluation

So are optimistic parallel order books possible? Yes!

Should they be used? Almost certainly not!

Unfortunately LMAX traditional thinking wins out this time, but perhaps I have helped you re-evaluate what you would think are inherently sequential systems using the power of time warp simulation, and rollbackable data structures.

If you have found any of this to be remotely interesting and would like to know more about discrete event simulation, and especially time warp simulation, I highly recommend you take the opportunity to read Parallel and Distributed Simulation Systems written by Professor Richard Fujimoto, so that you too can make disastrously messy order books…or rather wonderfully optimized airport simulations!